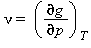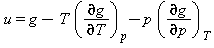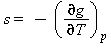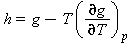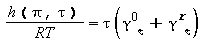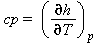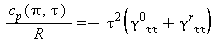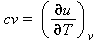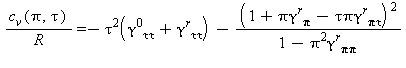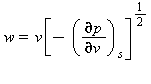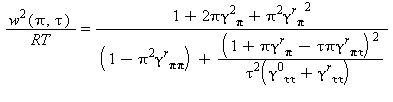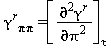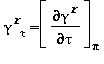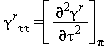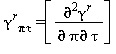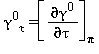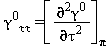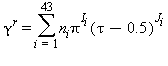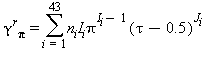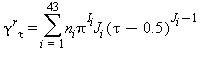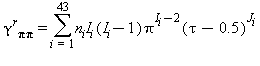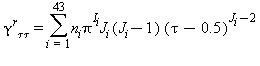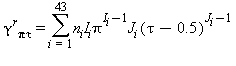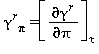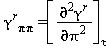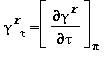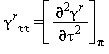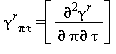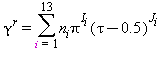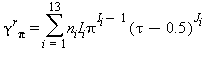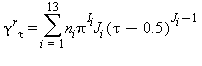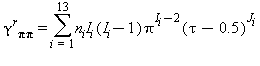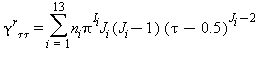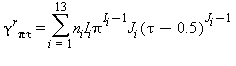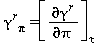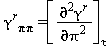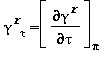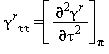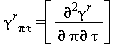Regione 2
- Categoria: IAPWS
- Pubblicato: Domenica, 27 Giugno 2010 06:26
- Scritto da Super User
- Visite: 8075
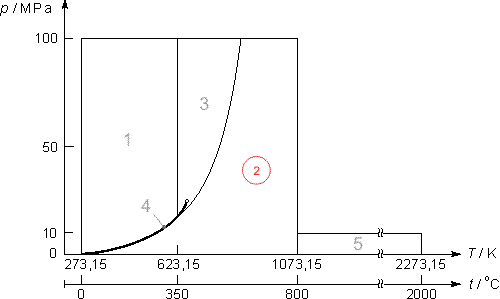
Equazioni di base
Le equazioni di base relative a questa regione coincidono con l’equazione fondamentale dell’energia libera di Gibbs g. Questa equazione espressa in forma adimensionale, γ=g/(RT), è divisa in due parti la prima si riferisce al gas ideale γ0 mentre la seconda alla parte residua γr :
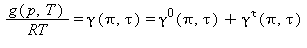 (15)
(15)
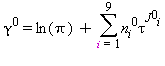 (16)
(16)
TABELLA 10
Valori dei coefficenti e degli esponenti della equazione adimensionale dell’energia libera di Gibbs relativi alla regione 2 come da eq. (16)
|
i
|
Ji0
|
ni0
|
i
|
Ji0
|
ni0
|
|
1a
|
0
|
-0.969 276 865 002 17 x 101
|
6
|
-2
|
0.142 408 191 714 44 x 101
|
|
2a
|
1
|
0.100 866 559 680 18 x 10²
|
7
|
-1
|
-0.438 395 113 194 50 x 101
|
|
3
|
-5
|
-0.560 879 112 830 20 x 10-²
|
8
|
2
|
-0.284 086 324 607 72
|
|
4
|
-4
|
0.714 527 380 814 55 x 10-1
|
9
|
3
|
0.212 684 637 533 07 x 10-1
|
|
5
|
-3
|
-0.407 104 982 239 28
|
|||
|
a Se l’eq. (16) e incorporata nell’eq. (18) i valori dei coefficenti n10 e n20 sono i seguenti:
n10=-0.969 372 683 930 49 x 101 n20=0.100 872 759 700 06 x 102
|
|||||
La parte della equazione (15) relativa alla parte residua γr è la seguente:
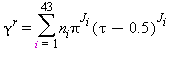 (17)
(17)
TABELLA 11
Valori dei coefficenti e degli esponenti della equazione della parte residua γr come da eq. (17)
|
i
|
I i
|
Ji
|
ni
|
|
1
|
1
|
0
|
-0.177 317 424 732 13 x 10-2
|
|
2
|
1
|
1
|
-0.178 348 622 923 58 x 10-1
|
|
3
|
1
|
2
|
-0.459 960 136 963 65 x 10-1
|
|
4
|
1
|
3
|
-0.575 812 590 834 32 x 10-1
|
|
5
|
1
|
6
|
-0.503 252 787 279 30 x 10-1
|
|
6
|
2
|
1
|
-0.330 326 416 702 03 x 10-4
|
|
7
|
2
|
2
|
-0.189 489 875 163 15 x 10-3
|
|
8
|
2
|
4
|
-0.393 927 772 433 55 x 10-2
|
|
9
|
2
|
7
|
-0.437 972 956 505 73 x 10-1
|
|
10
|
2
|
36
|
-0.266 745 479 140 87 x 10-4
|
|
11
|
3
|
0
|
0.204 817 376 923 09 x 10-7
|
|
12
|
3
|
1
|
0.438 706 672 844 35 x 10-6
|
|
13
|
3
|
3
|
-0.322 776 772 385 70 x 10-4
|
|
14
|
3
|
6
|
-0.150 339 245 421 48 x 10-2
|
|
15
|
3
|
35
|
-0.406 682 535 626 49 x 10-1
|
|
16
|
4
|
1
|
-0.788 473 095 593 67 x 10-9
|
|
17
|
4
|
2
|
0.127 907 178 522 85 x 10-7
|
|
18
|
4
|
3
|
0.482 253 727 185 07 x 10-6
|
|
19
|
5
|
7
|
0.229 220 763 376 61 x 10-5
|
|
20
|
6
|
3
|
-0.167 147 664 510 61 x 10-10
|
|
21
|
6
|
16
|
-0.211 714 723 213 55 x 10-2
|
|
22
|
6
|
35
|
-0.238 957 419 341 04 x102
|
|
23
|
7
|
0
|
-0.590 595 643 242 70 x 10-17
|
|
24
|
7
|
11
|
-0.126 218 088 991 01 x 10-5
|
|
25
|
7
|
25
|
-0.389 468 424 357 39 x 10-1
|
|
26
|
8
|
8
|
0.112 562 113 604 59 x 10-10
|
|
27
|
8
|
36
|
-0.823 113 408 979 98 x 101
|
|
28
|
9
|
13
|
0.198 097 128 020 88 x 10-7
|
|
29
|
10
|
4
|
0.104 069 652 101 74 x 10-18
|
|
30
|
10
|
10
|
-0.102 347 470 959 29 x 10-12
|
|
31
|
10
|
14
|
-0.100 181 793 795 11 x 10-8
|
|
32
|
16
|
29
|
-0.808 829 086 469 85 x 10-10
|
|
33
|
16
|
50
|
0.106 930 318 749 09
|
|
34
|
18
|
57
|
-0.336 622 505 741 71
|
|
35
|
20
|
20
|
0.891 858 453 554 21 x 10-24
|
|
36
|
20
|
35
|
0.306 293 168 762 32 x 10-12
|
|
37
|
20
|
48
|
-0.420 024 676 982 08 x 10-5
|
|
38
|
21
|
21
|
-0.590 560 296 865 39 x 10-25
|
|
39
|
22
|
53
|
0.378 269 476 134 57 x 10-5
|
|
40
|
23
|
39
|
-0.127 686 089 346 81 x 10-14
|
|
41
|
24
|
26
|
0.730 876 105 950 61 x 10-28
|
|
42
|
24
|
40
|
0.554 147 153 507 78 x 10-16
|
|
43
|
24
|
58
|
-0.943 697 072 412 10 x 10-6
|
TABELLA 12
Relazioni tra le varie proprietà termodinamiche sia la parte del gas-ideale γ0 sia la parte residua γrcome da eq. (15) e (18)
|
Proprietà |
Relazione |
|
|
Volume specifico |
|
|
|
Energia specifica interna |
|
|
|
Entropia specifica |
|
|
|
Entalpia specifica |
|
|
|
Capacità termica massica a pressione costante |
|
|
|
Capacità termica massica a volume costante |
|
|
|
Velocità del suono |
|
|
|
|
||
TABELLA 13
Equazioni relative alla parte del gas-ideale γ0 come da eq. (16)
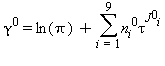 |
|
|
|
|
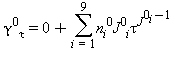 |
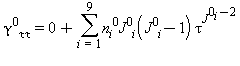 |
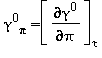 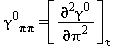 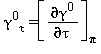 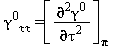 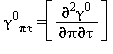 |
TABELLA 14
Equazioni relative alla parte residua γr come da eq. (17)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Intervallo di validità
L’equazione (15) è valida per i seguenti valori di temperatura T e pressione p:
273.15 K ≤ T ≤ 623.15 K ; 0 < p ≤ ps(T)eq.(30)
623.15 K < T ≤ 863.15 K ; 0 < p ≤ p(T)eq.(5)
863.15 K < T ≤ 1073.15 K ; 0 < p ≤ 100 MPa
Inoltre le proprietà calcolate per la fase vapore ottenuti mediante l’eq.(15) possono essere valide anche nelle fasi intermedie, fase vapore metastabile, solo per pressioni p oltre i 10 MPa mentre non sono valide per pressioni inferiori.
Test calcolo computer
La seguente tabella 15 contiene i valori di verifica relativi alla eq. (15).
TABELLA 15
Valori delle proprietà calcolati con l’eq. (15) in funzione di T e p
|
T= 300K
P= 0.0035 MPa
|
T= 700K
P = 0.00035 MPa
|
T = 700K
P = 30 MPa
|
|
|
v (m³·kg-1)
|
0.394 913 866 x 10²
|
0.923 015 898 x 10²
|
0.542 946 619 x 10²
|
|
h (kJ·kg-1)
|
0.254 991 145 x 104
|
0.333 568 375 x 104
|
0.263 149 474 x 104
|
|
u (kJ·kg-1)
|
0.241 169 160 x 104
|
0.301 262 819 x 104
|
0.246 861 076 x 104
|
|
s (kJ·kg-1·K-1)
|
0.852 238 967 x 10
|
0.101 749 966 x 10²
|
0.517 540 298 x 10
|
|
cp (kJ·kg-1·K-1)
|
0.191 300 162 x 10
|
0.208 141 274 x 10
|
0.103 505 092 x 10²
|
|
w (m·s-1)
|
0.427 920 172 x 10³
|
0.644 289 068 x 10³
|
0.480 386 523 x 10³
|
Equazione supplementari nel caso di fase vapore metastabile
Le equazioni supplementari nel caso di fase intermedia, detta fase vapore metastabile, relative a questa regione coincidono con l’equazione fondamentale dell’energia libera di Gibbs g. Questa equazione espressa in forma adimensionale, γ=g/(RT), è divisa in due parti la prima si riferisce al gas ideale γ0 mentre la seconda alla parte residua γr :
![]() (18)
(18)
L’equazione relativa alla parte del gas-ideale, γ0, è identica alla eq.(16) eccetto per i valori dei coefficenti n10 e n20 che variano come da leggenda tabella 10.
La parte relativa alla parte residua γr è descritta dalla seguente equazione:
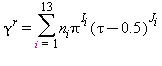 (19)
(19)
TABELLA 16
Valori dei coefficenti e degli esponenti della parte residua γr come da eq. (19)
|
i
|
Ii
|
Ji
|
ni
|
|
1
|
1
|
0
|
-0.733 622 601 865 06 x 10-2
|
|
2
|
1
|
2
|
-0.882 238 319 431 46 x 10-1
|
|
3
|
1
|
5
|
-0.723 345 552 132 45 x 10-1
|
|
4
|
1
|
11
|
-0.408 131 785 344 55 x 10-2
|
|
5
|
2
|
1
|
0.200 978 033 802 07 x 10-2
|
|
6
|
2
|
7
|
-0.530 459 218 986 42 x 10-1
|
|
7
|
2
|
16
|
-0.761 904 090 869 70 x 10-2
|
|
8
|
3
|
4
|
-0.634 980 376 573 13 x 10-2
|
|
9
|
3
|
16
|
-0.860 430 930 285 88 x 10-1
|
|
10
|
4
|
7
|
0.753 215 815 227 70 x 10-2
|
|
11
|
4
|
10
|
-0.792 383 754 461 39 x 10-2
|
|
12
|
5
|
9
|
-0.228 881 607 784 47 x 10-3
|
|
13
|
5
|
10
|
-0.264 565 014 828 10 x 10-2
|
TABELLA 17
Equazioni relative alla parte residua γr come da eq. (19)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Intervallo di validità
L’equazione (18) è valida nella fase vapore metastabile a partire dalla linea del vapore saturo fino alla linea che indica una miscela in equilibrio pari al 5% determinata con l’equilibrio dei valori di h’ e h’’ e con una pressione a partire dal triplo punto, vedi eq.(9), di oltre 10MPa.
Tolleranza numerica
I valori calcolati con l’eq.(18) con l’equazione di base, eq.(15), lungo la linea del vapore saturo devono avere una tolleranza massima per quanto riguarda v, h, cp, s, g e w di:
|Δv|max = 0.014 %
|Δh|max = 0.043 kJ·kg-1
|Δcp|max = 0.78 %
|Δs|max = 0.082 kJ·kg-1
|Δg|max = 0.023 kJ kg-1
|Δw|max = 0.051 %
Test calcolo computer
La seguente tabella 18 contiene i valori di verifica relativi alla eq. (18).
TABELLA 18
Proprietà termodinamiche calcolati con l’eq. (18) in funzione di T e p
|
T = 450K
p= 1 MPa
|
T = 440 K
p = 1 MPa
|
T= 450K
p= 1,5 MPa
|
|
|
v (m³·kg-1)
|
0.192 516 540
|
0.186 212 297
|
0.121 685 206
|
|
h (kJ·kg-1)
|
0.276 881 115 x 104
|
0.274 015 123 x 104
|
0.272 134 539 x 104
|
|
u (kJ kg-1)
|
0.257 629 461 x 104
|
0.255 393 894 x 104
|
0.253 881 758 x 104
|
|
s (kJ·kg-1·K-1)
|
0.656 660 377 x 101
|
0.650 218 759 x 101
|
0.629 170 440 x 101
|
|
cp (kJ·kg-1·K-1)
|
0.276 349 265 x 101
|
0.298 166 443 x 101
|
0.362 795 578 x 101
|
|
w (m·s-1)
|
0.498 408 101 x 103
|
0.489 363 295 x 103
|
0.481 941 819 x 103
|
Equazioni inverse
Per poter calcolare le proprietà con le equazioni inverse T(p,h) e T(p,s) con un errore di calcolo tollerabile bisogna suddividere la regione 2 in tre sottoregioni, chiamate subregioni, come da sottostante figura 2.
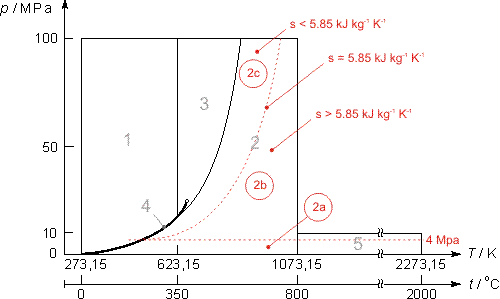
La linea che delimita le subregioni 2a e 2b è una isobara con una pressione p = 4 MPa mentre la curva che delimita le regioni 2b e 2c ha un valore di entropia s = 5.85 kJ·kg-1·K-1.
![]() (20)
(20)
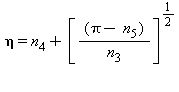 (21)
(21)
dove π e η sono uguali all’eq.(20) mentre i coefficenti n3 e n5 sono elencati nella seguente tabella 19.
TABELLA 19
Valori dei coefficenti dell’equazione B2bc come da eq. (20) e (21)
|
i
|
ni
|
i
|
ni
|
|
1
|
0,905 842 785 147 23 x 10³
|
4
|
0,265 265 719 084 28 x 104
|
|
2
|
-0,679 557 863 992 41
|
5
|
0,452 875 789 059 48 x 101
|
|
3
|
0,128 090 027 301 36 x 10-3
|
Intervallo di validità
Le equazioni (20) e (21) devono venire usate nell’intervallo corrispondente allo stato di saturazione tra T = 554.485 K con ps = 6.54670 MPa e T = 1019.32 K con p = 100 MPa.
Test calcolo computer
L’ eq.(20) e (21) devono verificare sia in p che in h il seguente singolo punto:
p = 0.100 000 000 x 103 MPa
h = 0.351 600 432 3 x 104 kJ·kg-1
Nel caso dell’equazione inversa T(p,s) dato che l’entropia s fa parte di una delle variabili di calcolo la scelta diventa automatica e quindi l’uso dell’eq.(20) e (21) è superfluo..
Per le equazioni inverse complete di indici e coefficenti fare riferimento alle rispettive subregioni 2a, 2b e 2c.

 Italian (IT)
Italian (IT)  English (UK)
English (UK)