Subregione 2a
- Categoria: IAPWS
- Pubblicato: Domenica, 27 Giugno 2010 06:27
- Scritto da Super User
- Visite: 8791
In questa sezione sono presenti solo le equazioni inverse T(p,h) e T(p,s) relative alla sola subregione 2a. Per tutte le altre informazioni (eq. fondamentali,eq. di base, ecc.) consultare la regione 2.
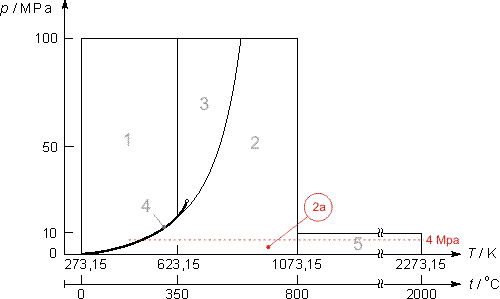
Equazione inversa T(p,h) subregione 2a
L’equazione inversa T(p,h) per la subregione 2a in forma adimensionale è la seguente:
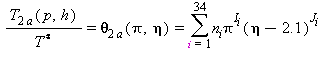 (22)
(22)
dove: θ=T/T*, p=p/p*, e η=h/h* con T*=1 K, p*=1 MPa, e h*=2000 kJ·kg-1.
I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 20a:
TABELLA 20a
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,h) relativa alla subregione 2a come da eq. (22)
|
i
|
Ii
|
Ji
|
ni
|
|
1
|
0
|
0
|
0.180 989 523 182 88 x 104
|
|
2
|
0
|
1
|
0.849 516 544 955 35 x 103
|
|
3
|
0
|
2
|
-0.107 817 480 918 26 x 103
|
|
4
|
0
|
3
|
0.331 536 548 012 63 x 102
|
|
5
|
0
|
7
|
-0.742 302 167 902 48 x 101
|
|
6
|
0
|
20
|
0.117 650 487 243 56 x 102
|
|
7
|
1
|
0
|
0.184 457 493 557 90 x 101
|
|
8
|
1
|
1
|
-0.417 927 005 496 24 x 101
|
|
9
|
1
|
2
|
0.624 781 969 358 12 x 101
|
|
10
|
1
|
3
|
-0.173 445 631 081 14 x 102
|
|
11
|
1
|
7
|
-0.200 581 768 620 96 x 103
|
|
12
|
1
|
9
|
0.271 960 654 737 96 x 103
|
|
13
|
1
|
11
|
-0.455 113 182 858 18 x 103
|
|
14
|
1
|
18
|
0.309 196 886 047 55 x 104
|
|
15
|
1
|
44
|
0.252 266 403 578 72 x 106
|
|
16
|
2
|
0
|
-0.617 074 228 683 39 x 10-2
|
|
17
|
2
|
2
|
-0.310 780 466 295 83
|
|
18
|
2
|
7
|
0.116 708 730 771 07 x 102
|
|
19
|
2
|
36
|
0.128 127 984 040 46 x 109
|
|
20
|
2
|
38
|
-0.985 549 096 23 76 x 109
|
|
21
|
2
|
40
|
0.282 245 469 730 02 x 1010
|
|
22
|
2
|
42
|
-0.359 489 714 107 03 x 1010
|
|
23
|
2
|
44
|
0.172 273 499 131 97 x 1010
|
|
24
|
3
|
24
|
-0.135 513 342 407 75 x 105
|
|
25
|
3
|
44
|
0.128 487 346 646 50 x 108
|
|
26
|
4
|
12
|
0.138 657 242 832 26 x 101
|
|
27
|
4
|
32
|
0.235 988 325 565 14 x 106
|
|
28
|
4
|
44
|
-0.131 052 365 450 54 x 108
|
|
29
|
5
|
32
|
0.739 998 354 747 66 x 104
|
|
30
|
5
|
36
|
-0.551 966 970 300 60 x 106
|
|
31
|
5
|
42
|
0.371 540 859 962 33 x 107
|
|
32
|
6
|
34
|
0.191 277 292 396 60 x 105
|
|
33
|
6
|
44
|
-0.415 351 648 356 34 x 106
|
|
34
|
7
|
28
|
-0.624 598 551 925 07 x 102
|
Intervallo di validità
L’equazione (22) è valida solo per la subregione 2a e quindi sono escluse le regioni in fase vapore metastabile. La pressione piu bassa per l’eq.(22) ammonta a 611.153 Pa a cui corrisponde una temperatura di sublimazione pari a 273.15 K.
Tolleranza numerica
Per almeno 106 valori random calcolati in p ed in h la differenza ΔT tra le temperature calcolate con l’eq. (22) e l’eq. (15) devono soddisfare i seguenti criteri:
|ΔT|tol = 10 mK ; |ΔT|max = 9.3 mK ; ΔTrms = 2.9 mK
Test calcolo computer
La seguente tabella 22a contiene i valori di verifica relativi alla eq. (22).
TABELLA 22a
Valori delle temperature calcolati con l’eq. (22) in funzione di p e h
|
p (MPa)
|
h (kJ·kg-1)
|
T (K)
|
|
0.001
|
3000
|
0.534 433 241 x 103
|
|
3
|
3000
|
0.575 373 370 x 103
|
|
3
|
4000
|
0.101 077 577 x 104
|
Equazione inversa T(p,s) subregione 2a
L’equazione inversa T(p,s) per la subregione 2a in forma adimensionale è la seguente:
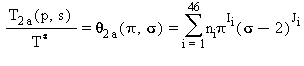 (25)
(25)
dove: θ=T/T*, p=p/p*, e σ=s/s* con T*=1 K, p*=1 MPa, e s*=2 kJ·kg-1·K-1.
I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 21a:
TABELLA 21a
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,s) relativa alla regione 2a come da eq. (25)
|
I
|
Ii
|
Ji
|
ni
|
|
1
|
-1,5
|
-24
|
-0,392 359 838 619 84 x 106
|
|
2
|
-1,5
|
-23
|
0,515 265 738 272 70 x 106
|
|
3
|
-1,5
|
-19
|
0,404 824 431 610 48 x 105
|
|
4
|
-1,5
|
-13
|
-0,321 937 909 239 02 x 103
|
|
5
|
-1,5
|
-11
|
0,969 614 242 186 94 x 102
|
|
6
|
-1,5
|
-10
|
-0,228 678 463 717 73 x 102
|
|
7
|
-1,25
|
-19
|
-0,449 429 141 243 57 x 106
|
|
8
|
-1,25
|
-15
|
-0,501 183 360 201 66 x 104
|
|
9
|
-1,25
|
-6
|
0,356 844 635 600 15
|
|
10
|
-1,0
|
-26
|
0,442 353 358 481 90 x 105
|
|
11
|
-1,0
|
-21
|
-0,136 733 888 117 08 x 105
|
|
12
|
-1,0
|
-17
|
0,421 632 602 078 64 x 106
|
|
13
|
-1,0
|
-16
|
0,225 169 258 374 75 x 105
|
|
14
|
-1,0
|
-9
|
0,474 421 448 656 46 x 103
|
|
15
|
-1,0
|
-8
|
-0,149 311 307 976 47 x 103
|
|
16
|
-0,75
|
-15
|
-0,197 811 263 204 52 x 106
|
|
17
|
-0,75
|
-14
|
-0,235 543 994 707 60 x 105
|
|
18
|
-0,5
|
-26
|
-0,190 706 163 020 76 x 105
|
|
19
|
-0,5
|
-13
|
0,553 756 698 831 64 x 105
|
|
20
|
-0,5
|
-9
|
0,382 936 914 373 63 x 104
|
|
21
|
-0,5
|
-7
|
-0,603 918 605 805 67 x 103
|
|
22
|
-0,25
|
-27
|
0,193 631 026 203 31 x 104
|
|
23
|
-0,25
|
-25
|
0,426 606 436 986 10 x 104
|
|
24
|
-0,25
|
-11
|
-0,597 806 388 727 18 x 104
|
|
25
|
-0,25
|
-6
|
-0,704 014 639 268 62 x 103
|
|
26
|
0,25
|
1
|
0,338 367 841 075 53 x 103
|
|
27
|
0,25
|
4
|
0,208 627 866 351 87 x 102
|
|
28
|
0,25
|
8
|
0,338 341 726 561 96 x 10-1
|
|
29
|
0,25
|
11
|
-0,431 244 284 148 93 x 10-4
|
|
30
|
0,50
|
0
|
0,166 537 913 564 12 x 103
|
|
31
|
0,5
|
1
|
-0,139 862 920 558 98 x 103
|
|
32
|
0,5
|
5
|
-0,788 495 479 998 72
|
|
33
|
0,5
|
6
|
0,721 324 117 538 72 x 10-1
|
|
34
|
0,5
|
10
|
-0,597 548 393 982 83 x 10-2
|
|
35
|
0,5
|
14
|
-0,121 413 589 539 04 x 10-4
|
|
36
|
0,5
|
16
|
0,232 270 967 338 71 x 10-6
|
|
37
|
0,75
|
0
|
-0,105 384 635 661 94 x 102
|
|
38
|
0,75
|
4
|
0,207 189 254 965 02 x 101
|
|
39
|
0,75
|
9
|
-0,721 931 552 604 27 x 10-1
|
|
40
|
0,75
|
17
|
0,207 498 870 811 20 x 10-6
|
|
41
|
1,0
|
7
|
-0,183 406 579 113 79 x 10-1
|
|
42
|
1,0
|
18
|
0,290 362 723 486 96 x 10-6
|
|
43
|
1,25
|
3
|
0,210 375 278 936 19
|
|
44
|
1,25
|
15
|
0,256 812 397 299 99 x 10-3
|
|
45
|
1,5
|
5
|
-0,127 990 029 337 81 x 10-1
|
|
46
|
1,5
|
18
|
-0,821 981 026 520 18 x 10-5
|
Intervallo di validità
L’equazione (25) è valida solo per la subregione 2a e quindi sono escluse le regioni in fase vapore metastabile. La pressione piu bassa per l’eq.(25) ammonta a 611.153 Pa a cui corrisponde una temperatura di sublimazione pari a 273.15 K.
Tolleranza numerica
Per almeno 106 valori random calcolati in p ed in s la differenza ΔT tra le temperature calcolate con l’eq. (25) e l’eq. (15) devono soddisfare i seguenti criteri:
|ΔT|tol = 10 mK ; |ΔT|max = 8.8 mK ; ΔTrms = 1.2 mK
Test calcolo computer
La seguente tabella 23a contiene i valori di verifica relativi alla eq. (25).
TABELLA 23a
Valori delle temperature calcolati con l’eq. (25) in funzione di p e s
|
p (MPa)
|
s (kJ·kg-1·K-1)
|
T (K)
|
|
0.1
|
7.5
|
0.399 517 097 x 103
|
|
0.1
|
8
|
0.514 127 081 x 103
|
|
2.5
|
8
|
0.103 984 917 x 104
|

 Italian (IT)
Italian (IT)  English (UK)
English (UK)