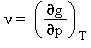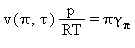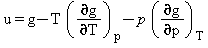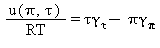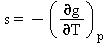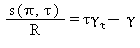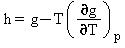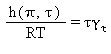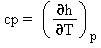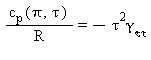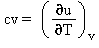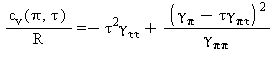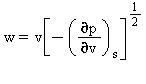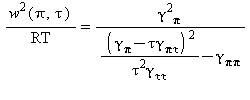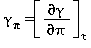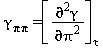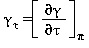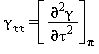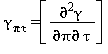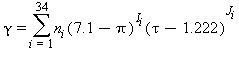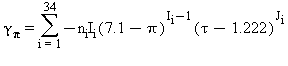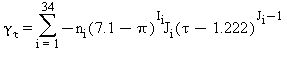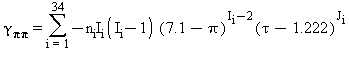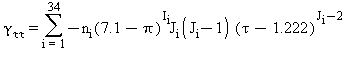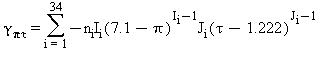ASSISTENZA - Essica Srl Macchine ed impianti per pastifici - Fresh and Precooked Pasta Lines

1Richiedi le credenziali a info@essica.it
2Verifica la tua email
3Inserisci nel LOGIN le tue credenziali

Per qualsiasi problema inviaci una email a info@essica.it. Grazie!

Orario uffici

Lunedì-Venerdì  9:00AM - 12:00AM
                      14:00PM - 17:00PM
Sabato solo su appuntamento!

CREA IL TUO ACCOUNT

*

*

*

*

*

*

ESISTE GIA QUESTO ACCOUNT?

HAI PERSO LA TUA PASSWORD?

*

AAH, WAIT, I REMEMBER NOW!
Sunday Sep 15th, 2024

Regione 1

Category: IAPWS
Published: Sunday, 27 June 2010 06:25
Written by Super User
Hits: 8235
 

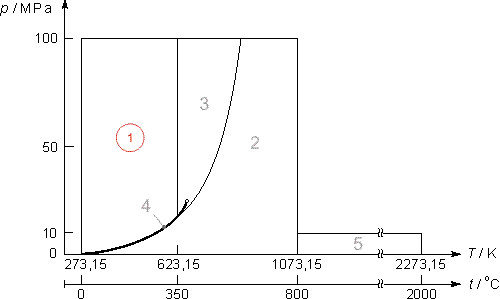
Equazioni di base

Le equazioni di base relative a questa regione coincidono con l’equazione fondamentale dell’energia libera di Gibbs g. Questa equazione espressa in forma adimensionale, γ=g/(RT), si legge: 

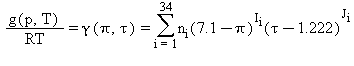(7)

dove p=p/p* e t=T*/T con p*=16.53 MPa, T*=1386 K, R=0.461526 kJ/(kg·K)
I coefficenti ni e gli esponenti Ii e Ji sono elencati nella seguente tabella 2. 

TABELLA 2
Valori dei coefficenti e degli esponenti della equazione adimensionale dell’energia libera di Gibbs relativi alla regione 1 come da eq. (7)

i
Ii
Ji
ni
1
0
-2
0.146 329 712 131  67
2
0
-1
-0.845 481 871 691 14
3
0
0
-0.375 636 036 720 40 x 101
4
0
1
0.338 551 691 683 85 x 101
5
0
2
-0.957 919 633 878 72
6
0
3
0.157 720 385 132 28
7
0
4
-0.166 164 171 995 01 x 10-1
8
0
5
0.812 146 299 835 68 x 10-3
9
1
-9
0.283 190 801 238 04 x 10-3
10
1
-7
-0.607 063 015 658 74 x 10-3
11
1
-1
-0.189 900 682 184 19 x 10-1
12
1
0
-0.325 297 487 705 05 x 10-1
13
1
1
-0.218 417 171 754 14 x 10-1
14
1
3
-0.528 383 579 699 30 x 10-4
15
2
-3
-0.471 843 210 732 67 x 10-3
16
2
0
-0.300 017 807 930 26 x 10-3
17
2
1
0.476 613 939 069 87 x 10-4
18
2
3
-0.441 418 453 308 46 x 10-5
19
2
17
-0.726 949 962 975 94 x 10-15
20
3
-4
-0.316 796 448 450 54 x 10-4
21
3
0
-0.282 707 979 853 12 x 10-5
22
3
6
-0.852 051 281 201 03 x 10-9
23
4
-5
-0.224 252 819 080 00 x 10-5
24
4
-2
-0.651 712 228 956 01 x 10-6
25
4
10
-0.143 417 299 379 24 x 10-12
26
5
-8
-0.405 169 968 601 17 x 10-6
27
8
-11
-0.127 343 017 416 41 x 10-8
28
8
-6
-0.174 248 712 306 34 x 10-9
29
21
-29
-0.687 621 312 955 31 x 10-18
30
23
-31
0.144 783 078 285 21 x 10-19
31
29
-38
0.263 357 816 627 95 x 10-22
32
30
-39
-0.119 476 226 400 71 x 10-22
33
31
-40
0.182 280 945 814 04 x 10-23
34
32
-41
-0.935 370 872 924 58 x 10-25

Tutte le proprietà termodinamiche sono derivate dall’equazione (7) con la corretta combinazione degli indici relativi alla energia libera di Gibbs e relative derivate. Le proprietà più importanti incluso γ e relative derivate sono elencati nella tabella 3 mentre tutte le derivate relative all’energia libera di Gibbs sono elencate nella tabella 4. 

Durante la 5th conferenza internazionale sulle proprietà del vapore tenutasi a Londra nel 1956 si definì che l’energia interna specifica e l’entropia specifica del liquido in saturazione nel triplo punto siano uguali a zero: 
u’t=0  ;  s’t=0 
ne deriva che il triplo punto si trova alle seguenti condizioni di temperatura assoluta T e pressione p: 
Tt=273.16 K  ;  pt=611.657 Pa
Di conseguenza l’entalpia specifica relativa al liquido in saturazione nel triplo punto risulta in base all’eq. (7):
h’t=0.611783 J/kg 

TABELLA 3
Relazioni tra le varie proprietà termodinamiche come da eq. (7)

Proprietà

Relazione

Volume specifico

Energia specifica interna

Entropia specifica

Entalpia specifica

Capacità termica massica a pressione costante

Capacità termica massica a volume costante

Velocità del suono

TABELLA 4
Relazioni tra le varie proprietà termodinamiche come da eq. (7)

Intervallo di validità

L’equazione (7) è valida per i seguenti valori di temperatura T e pressione p:

273.15 K ≤ T ≤ 623.15 K

ps(T) ≤ p ≤ 100 MPa

Test calcolo computer

La seguente tabella 5 contiene i valori di verifica relativi alla eq. (7).

TABELLA 5
Valori delle proprietà calcolati con l’eq. (7) in funzione di T e p

 
T = 300 K
p=3 MPa
T = 300 K
p=80 MPa
T = 500 K
p=3 MPa
v (m3·kg-1)
0.100 215 168 x 10-2
0.971 180 894 x 10-3
0.120 241 800 x 10-2
h (kJ·kg-1)
0.115 331 273 x 103
0.184 142 828 x 103
0.975 542 239 x 103
u (kJ·kg-1)
0.112 324 818 x 103
0.106 448 356 x 103
0.971 934 985 x 103
s (kJ·kg-1·K-1)
0.392 294 792
0.368 563 852
0.258 041 912 x 101
cp (kJ·kg-1·K-1)
0.417 301 218 x 101
0.401 008 987 x 101
0.465 580 682 x 101
w (m·s-1)
0.150 773 921 x 104
0.163 469 054 x 104
0.124 071 337 x 104

Equazione inversa T(p,h)

L’equazione inversa T(p,h) per la regione 1 in forma adimensionale è la seguente:

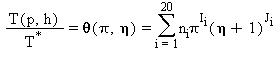(11)

dove: θ=T/T*,   p=p/p*, s=s/s*, e η=h/h* con T*=1 K, p*=1 MPa, e h*=2500 kJ·kg-1.

I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 6:

TABELLA 6
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,h) relativa alla regione 1 come da eq. (11)

i
Ii
Ji
ni
1
0
0
-0.238 724 899 245 21 x 103
2
0
1
0.404 211 886 379 45 x 103
3
0
2
0.113 497 468 817 18 x 103
4
0
6
-0.584 576 160 480 39 x 101
5
0
22
-0.152 854 824 131 40 x 10-3
6
0
32
-0.108 667 076 953 77 x 10-5
7
1
0
-0.133 917 448 726 02 x 102
8
1
1
0.432 110 391 835 59 x 102
9
1
2
-0.540 100 671 705 06 x 102
10
1
3
0.305 358 922 039 16 x 102
11
1
4
-0.659 647 494 236 38
12
1
10
0.939 654 008 783 63 x 10-2
13
1
32
0.115 736 475 053 40 x 10-6
14
2
10
-0.258 586 412 820 73 x 10-4
15
2
32
-0.406 443 630 847 99 x 10-8
16
3
10
0.664 561 861 916 35 x 10-7
17
3
32
0.806 707 341 030 27 x 10-10
18
4
32
-0.934 777 712 139 47 x 10-12
19
5
32
0.582 654 420 206 01 x 10-14
20
6
32
-0.150 201 589 535 03 x 10-16

Intervallo di validità

L’equazione (11) è valida per lo stesso intervallo dell’equazione di base (7) eccetto per la regione intermedia (liquido surriscaldato) dove risulta non valida.

Tolleranza numerica

Per almeno 106 valori random calcolati in p ed in h la differenza ΔT tra le temperature calcolate con l’eq. (11) e l’eq. (7) devono soddisfare i seguenti criteri:

|ΔT|tol = 25 mK   ;   ΔTrms = 13.4 mK   ;  |ΔT|max = 23.6 mK

Test calcolo computer

La seguente tabella 7 contiene i valori di verifica relativi alla eq. (11).

TABELLA 7
Valori delle temperature calcolati con l’eq. (11) in funzione di p e h

p (MPa)
h (kJ·kg-1)
T (K)
3
500
0.391 798 509 x 103
80
500
0.378 108 626 x 103
80
1500
0.611 041 229 x 103

Equazione inversa T(p,s)

L’equazione inversa T(p,s) per la regione 1 in forma adimensionale è la seguente:

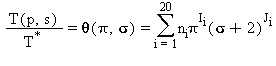(13)

dove: θ=T/T*,   p=p/p*, e s=s/s* con T*=1 K, p*=1 MPa, e s*=1 kJ·kg-1·K-1.

I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 8:

TABELLA 8
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,s) relativa alla regione 1 come da eq. (13)

i
Ii
Ji
ni
1
0
0
0.174 782 680 583 07 x 103
2
0
1
0.348 069 308 928 73 x 102
3
0
2
0.652 925 849 784 55 x 101
4
0
3
0.330 399 817 754 89
5
0
11
-0.192 813 829 231 96 x 10-6
6
0
31
-0.249 091 972 445 73 x 10-22
7
1
0
-0.261 076 364 893 32
8
1
1
0.225 929 659 815 86
9
1
2
-0.642 564 633 952 26 x 10-1
10
1
3
0.788 762 892 705 26 x 10-2
11
1
12
0.356 721 106 073 66 x 10-9
12
1
31
0.173 324 969 948 95 x 10-23
13
2
0
0.566 089 006 548 37 x 10-3
14
2
1
-0.326 354 831 397 17 x 10-3
15
2
2
0.447 782 866 906 32 x 10-4
16
2
9
-0.513 221 569 085 07 x 10-9
17
2
31
-0.425 226 570 422 07 x 10-25
18
3
10
0.264 004 413 606 89 x 10-12
19
3
32
0.781 246 004 597 23 x 10-28
20
4
32
-0.307 321 999 036 68 x 10-30

L’equazione (13) è valida per lo stesso intervallo dell’equazione di base (7) eccetto per la regione intermedia (liquido surriscaldato) dove risulta non valida.

Tolleranza numerica

Per almeno 106 valori random calcolati in p ed in s la differenza ΔT tra le temperature calcolate con l’eq. (13) e l’eq. (7) devono soddisfare i seguenti criteri:

|ΔT|tol = 25 mK   ;   ΔTrms = 5.8 mK   ;  |ΔT|max = 21.8 mK

Test calcolo computer

La seguente tabella 9 contiene i valori di verifica relativi alla eq. (13).

TABELLA 9
Valori delle temperature calcolati con l’eq. (13) in funzione di p e s

p (MPa)
s (kJ·kg-1·K-1)
T (K)
3
0.5
0.307 842 258 x 103
80
0.5
0.309 979 785 x 103
80
3
0.565 899 909 x 103
TOP