Regione 4
- Category: IAPWS
- Published: Sunday, 27 June 2010 06:32
- Written by Super User
- Hits: 8573
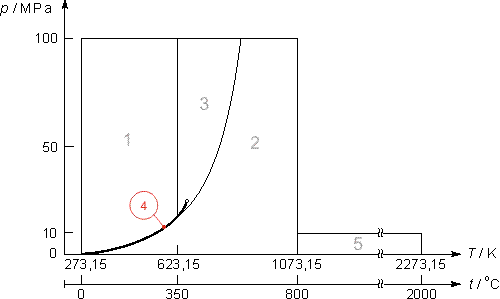
Equazioni fondamentali
L’equazione fondamentale che descrive la curva di saturazione, regione 4, che verrà usata successivamente per le equazioni di base e per le equazioni inverse è la seguente:
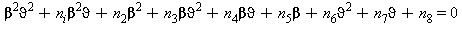 (29)
(29)
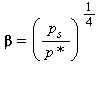 (29a)
(29a)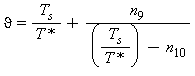 (29b)
(29b)Equazioni di base (calcolo pressione di saturazione ps)
L’equazione fondamentale (29) risolta in funzione della pressione di saturazione ps risulta:
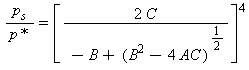 (30)
(30)
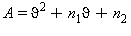
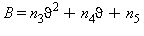
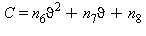
TABELLA 34
Valori dei coefficenti come da eq. (29) fino eq.(31)
|
i
|
ni
|
i
|
ni
|
|
1
|
0.116 705 214 527 67 x 104
|
6
|
0.149 151 086 135 30 x 102
|
|
2
|
-0.724 213 167 032 06 x 106
|
7
|
-0.482 326 573 615 91 x 104
|
|
3
|
-0.170 738 469 400 92 x 102
|
8
|
0.405 113 405 420 57 x 106
|
|
4
|
0.120 208 247 024 70 x 105
|
9
|
-0.238 555 575 678 49
|
|
5
|
-0.323 255 503 223 33 x 107
|
10
|
0.650 175 348 447 98 x 103
|
Intervallo di validità
Le equazioni che vanno dall’eq.(29) fino all’eq.(31) riproducono esattamente la relazione p-T; e il valore del triplo punto è in accordo con l’eq.(8) e con il punto normale di ebolizione (12) mentre il punto critico risulta in accordo con l’eq.(2) e (3). Inoltre l’eq.(30) è valida lungo tutta la curva che descrive il limite liquido-vapore a partire dal triplo punto, a cui corrisponde la temperatura Tt , fino al punto critico, a cui corrisponde una temperatura Tc , pertanto l’intervallo, in funzione di T, risulta:
273.15 K ≤ T ≤ 647.096 K
Test calcolo computer
La seguente tabella 35 contiene i valori di verifica relativi alla eq. (30).
TABELLA 35
Proprietà termodinamiche calcolati con l’eq. (30) in funzione di T
|
T (K)
|
ps (MPa)
|
|
300
|
0.353 658 941 x 10-2
|
|
500
|
0.263 889 776 x 10-1
|
|
600
|
0.123 443 146 x 102
|
Equazioni inverse (calcolo temperatura di saturazione Ts)
L’equazione fondamentale (29) risolta in funzione della temperatura di saturazione Ts risulta:
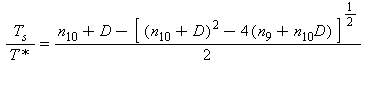 (31)
(31)
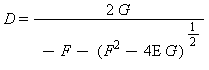
dove le variabili E, F, e G sono le seguenti:
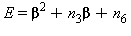
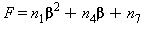
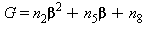
Intervallo di validità
L’equazione (31) ha lo stesso intervallo di validita dell’eq.(30) a cui corrisponde il seguente intervallo di pressione p:
611.213 Pa ≤ p ≤ 22.064 MPa
Test calcolo computer
La seguente tabella 36 contiene i valori di verifica relativi alla eq. (31).
TABELLA 36
Proprietà termodinamiche calcolati con l’eq. (31) in funzione di p
|
p (MPa)
|
Ts (K)
|
|
0.1
|
0.372 755 919 x 103
|
|
1
|
0.453 035 632 x 103
|
|
10
|
0.584 149 488 x 103
|

 Italian (IT)
Italian (IT)  English (UK)
English (UK)